微积分导论课程的重点和主题涉及科学、工程和商业领域中最重要的数学应用基础。课程强调微积分的关键思想和历史动机,同时在理论和应用之间取得平衡,从而掌握基础数学中的关键门槛概念。
了解顶级公司的员工如何掌握热门技能

该课程共有5个模块
本单元首先介绍实数线上的各种数、十进制展开式和近似值,然后继续探索方程和不等式的运算、符号图和直角坐标平面的使用。
涵盖的内容
10个视频8篇阅读材料9个作业
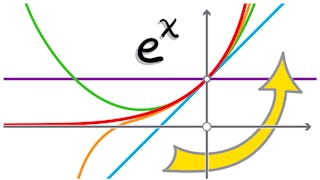
本单元介绍了函数的概念,它准确地捕捉了不同数量或测量值之间的联系。 本模块涵盖二次函数、三次函数、一般幂函数和多项式函数;指数函数和对数函数;以及与周期行为数学相关的三角函数。 我们利用组合和反转创建新函数,并研究如何通过 xy 平面上的变换,在代数和视觉上在不同数量之间前后移动。
涵盖的内容
13个视频12篇阅读材料13个作业
本单元介绍微分学技术。我们研究平均变化率,当时间间隔变得非常小时,平均变化率就会变成瞬时变化率,从而引出导数的概念。然后,我们探索利用切线的微分技术。本单元介绍莱布尼兹符号,并说明如何使用它来轻松获取函数导数的信息以及如何应用它。
涵盖的内容
12个视频10篇阅读材料11个作业
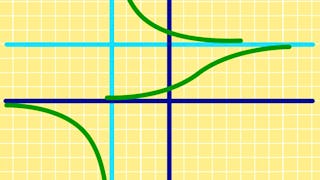
本模块继续微分学的发展,介绍函数的一阶导数和二阶导数。 我们使用一阶导数和二阶导数的符号图,并由此开发出系统的曲线勾画协议。本模块还介绍了利用链式法则、积式法则和商式法则寻找由较简单函数建立的复杂函数导数的规则,以及如何利用导数信息解决困难的优化问题。
涵盖的内容
14个视频13篇阅读材料14个作业
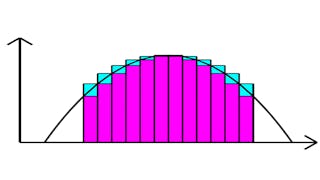
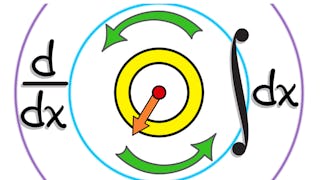
第五也是最后一个单元介绍积分微积分,研究切线的斜率和曲线下的面积。 由此引出微积分基本定理。我们探索利用速度曲线下的面积来估算位移,使用的是下矩形近似值和上矩形近似值的平均值。然后,我们研究近似值的极限,发现圆面积和抛物线下面积的公式。 然后,我们利用黎曼和与定积分,开发精确捕捉曲线下面积的方法。然后,本单元将介绍不定积分和代入积分法。最后,我们将讨论与旋转对称和反射对称有关的奇函数和偶函数的性质,以及修正指数增长的对数函数。
涵盖的内容
14个视频10篇阅读材料9个作业
位教师

从 数学与逻辑 浏览更多内容
The University of Sydney
 状态:预览
状态:预览The Hong Kong University of Science and Technology
 状态:免费
状态:免费University of Pennsylvania
 状态:免费
状态:免费University of Pennsylvania
人们为什么选择 Coursera 来帮助自己实现职业发展




学生评论
3,916 条评论
- 5 stars
87.13%
- 4 stars
10.30%
- 3 stars
1.14%
- 2 stars
0.56%
- 1 star
0.84%
显示 3/3916 个
已于 Aug 29, 2020审阅
Exceptional course. Fantastic explaining by Professor Easdown, I wish more teachers were as clear as he is, and as kind and thoughtful towards their students. Many, many thanks in case you see this.
已于 Jul 20, 2020审阅
The course is amazing, the teacher is incredible that makes the course be cooler and easier to do it. I enjoyed a lot the experience and certainly will help me to develop my professional career.
已于 Apr 2, 2020审阅
Amazing Explanations..... I love how the course is sequenced and it provides not only the mechanical solutions to calculus but also the theories behind each module and topics... Great Course
常见问题
要获取课程资料、作业和证书,您需要在注册课程时购买证书体验。 您可以尝试免费试听,或申请资助。课程可能提供 "完整课程,无证书"。通过该选项,您可以查看所有课程资料,提交必要的评估,并获得最终成绩。这也意味着您无法购买证书体验。
购买证书后,您就可以访问所有课程资料,包括已评分的作业。完成课程后,您的电子证书将添加到您的 "成就 "页面--您可以从那里打印证书或将其添加到您的 LinkedIn 个人资料中。
是的。在特定的学习课程中,如果您付不起注册费,可以申请助学金或奖学金。如果您选择的学习课程有助学金或奖学金,您可以在说明页面找到申请链接。
更多问题
提供助学金,






